Simple Harmonic Motion
Simple Harmonic Motion: Overview
This Topic covers sub-topics such as Simple Harmonic Motion, Amplitude, Phase, Angular Frequency, Equation of SHM, Mean Position, Initial Phase, Phase Difference in SHM, Initial Phase Calculation, Extreme positions in SHM and, Position-Time Graph in SHM
Important Questions on Simple Harmonic Motion
The work done by the tension in the string of a simple pendulum in one complete oscillation is equal to
Displacement of a particle is given by . Is it simple harmonic? If so, what is its period?
A simple pendulum completes oscillations in and go to a maximum distance of from its rest position. If at the start of the motion, the pendulum has angular displacement of rad to the right of its rest position. Write the displacement equation of the pendulum.
The graph of a particle undergoing simple harmonic motion is as shown in the figure.
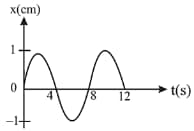
The acceleration of the particle at is
What will be the initial phase of simple harmonic motion represented by the equation .
Two particles are performing SHM in same phase. It means that:
If two SHMs of different amplitudes are added together, the resultant SHM will be a maximum if the phase difference between them is:
Two particles execute simple harmonic motions of same amplitude and frequency along the same straight line. They cross one another when going opposite directions. The phase difference between them when their displacements are one half of their amplitudes is then:
Initial phase of the particle executing SHM with is:
In simple harmonic motion, potential energy value at extreme position is _____.
In simple harmonic motion, At the extreme position kinetic energy is zero.
Which one of this will be zero at extreme position of simple harmonic motion?
When two particles executing SHM are overlapped in opposite phase then resultant amplitude will be
A is the amplitude, ω is the angular frequency, and φ is called the _____.
The displacement of two particles executing SHM are expressed as and then at both are
When two SHMS are super imposed so that resultant amplitude becomes minimum then both are overlapped in _____ phase?
Two simple harmonic motions have displacements and are superimposed on each other. Resulting amplitude will be.
